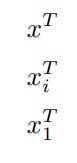Demystifying Elements of Statistical Learning - Stats Post Pt. 1
Covering Introduction - Chapter 2.3.1 Linear Models and Least Squares Included
The Elements of Statistical of Learning: Data Mining, Inference, and Prediction by Trevor Hastie, Robert Tibshirani and Jerome Friedman is an excellent book on statistics and many of statistics’ applications. A few years back, looking to enhance my understanding of statistics, I tried to read the book and quickly gave up due to the subject’s difficulty, and the book’s often dense and mathematical language. Earlier this year, I asked some of my smartest friends about enhancing my statistical understanding, and this book was top of the list again. It’s seen as one of the best books on the subject, and I find that it has really improved my statistical thinking and really quickly too. But again, it’s also quite hard.
Who is this for and why would you want to follow along with this series?
In short, everyone. I’m being a bit glib, but statistics are all around us all the time. Understanding how to formulate a stats-related problem, and then how you might test it is extremely valuable. Huge swathes of every field fall under this. This has applications in medicine, finance, machine learning (many of the techniques are gone over directly in this book), economics, mathematics, sports, etc. - honestly almost any field you can think of, there are numbers somewhere, and knowing what you can (and can’t!) conclude from those numbers is very valuable. Furthermore, it will help you in your daily life - the more that I have grasped of this book, the more I am able to understand the arguments others are making, and how much value I should place in those arguments. Compared to before I started this book a second time, I now am able to read more news articles and academic studies and actually feel like I can asses claims made in a way I couldn’t previously.
But you’re already reading, and are probably worried about this book’s deserving reputation as dense and tough. I agree, but I also think that we can get through this together and gain its valued insights. As for my background, I work in finance, but am not what would be called a “quant.” I’m just a guy that took mathematics through calculus and that was a while ago. Sure I took some stats courses in college, but I promise you if you saw my grades you’d feel comfortable that we’re starting this journey from a relative novice’s perspective. I’ll try to write to folks on that level of understanding, but if you feel anything I write isn’t clear enough, please feel free to reach out and provide feedback. Everyone stands to learn here.
And I haven’t even gotten to the best part: all of this is free!
Yes! You can read the book for free (link below and here) and these posts are all free. I do usually post about sumo wrestling here too, but if you sign up I’ll make sure to preface all future posts with (Statistics) or (Sumo) in the title. That said, the sumo posts often apply lessons from here and some even have a highly statistical bent (this piece talks about Linear Regressions, and some possible pitfalls in fitting a model). I can’t promise a regular cadence of posts on this, but I will try my best to post at least semi-regularly, and selfishly, I’m also hoping this enhances my learning so I do have a good incentive to keep this up.
https://hastie.su.domains/ElemStatLearn/
How you use this? It’s up to you. But I think the best way would be to read the section covered, try to think on it and understand as best as you can (if little sticks, that’s not an issue!), then consult my notes and re-read. Sometimes it’s taken me a few times reading a sentence to grasp its meaning. That can be even with the notes, but think of your goal as developing a little more understanding. That adds up over time. And my one other recommendation is: when you feel you understand a section, that’s the best time to re-read it, so that your firm understanding sinks in all the deeper.
Today’s post we’ll learn the basics including the notation we expect to use, what we call our input and output, and then finishing off looking over a basic linear regression.
Let’s begin!
Preface & 1 Introduction
I would recommend reading both of these, but we’ll begin with:
2 Overview of Supervised Learning (page 9)
2.1 Introduction
We expect to have Inputs and then use that to predict Outputs
This is called Supervised Learning
Please note there is also Unsupervised Learning, but that’s a different topic
Inputs have many different terms we can use for them
Our inputs are variables
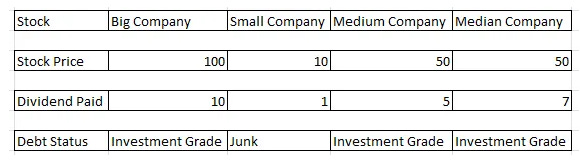
it might be Stock Prices = [100, 10, 50, 50] for instance
These terms are essentially interchangeable, but it is helpful to try and remember the different terms because they do come up in the book or in other literature (which is why we want to know them!)
Independent Variables
The emphasis is on Independent - if these variables are not independent from each other, it is liable to cause problems
Predictors
This is more common in the language of statistical literature
Features
This is used more often in pattern recognition literature
Outputs also have many different terms we can use for them
Again, the terms are fairly interchangeable but can differ from field to field
Dependent Variable
This term is actually very helpful. As we talked about above how our inputs should be independent our output depends on those inputs, and hence we call it the dependent variable.
Responses
In sumo wrestling, the wrestlers will be ranked each tournament based on how many matches they won the prior tournament. So to predict this, I would gather the data on how many matches wrestlers won in a tournament and use that as my Predictor or Feature. Our Response in this question would be their rank in the next tournament based off of those wins. So:
Feature (s) → model (what we’ll be learning) → Response
Wins in tournament at Time 0 (present) → model → Predicted Rank at Time t+1 (the following tournament)
If you want to check out the above problem I described, and see an actual example including discussion of how to setup the problem, it’s here.
2.2 Variable Types and Terminology (Page 9 through 11)
There are different types of output we can have. Furthermore, the different output types will dictate what we call the prediction task we’re working with (hopefully clearer below)
Quantitative Output
The output is numerical
Regression is the naming convention for these kinds of predictions
If we were trying to predict the amount of sales a pizza store will have in dollars, that would be a quantitative output, i.e. with our Independent Variables (economic data, neighborhood, etc.) we use a regression to predict the store will make $100,000 next month; that is quantitative output
Qualitative Output
The output can also be referred to as:
Categorical variables
Discrete variables
Factors
Classification is the naming convention for these kinds of predictions
If we had an image of text, we could try and use a Classification model to classify each letter in the text
i.e. the first letter in an image of the text is classified via our algorithm as “A”; that would be a qualitative output
Ordered Categorical
For instance: Small, Medium, Large
There is an ordering between them, but the differences between them aren’t generalizable such that it fits into a Quantitative or Qualitative
Using numerical codes for qualitative variables
When you have only two categories, like “buy a stock” or “do not buy that stock” then you can represent that as a 0 or a 1.
These are sometimes called targets
When there are more than two categories, you might use dummy variables
These are usually just a bunch of options where the variable is classified as a 0 or a 1
Let’s say I wanted to represent what size some companies are, and the categories are Small, Medium, and Large, then I can just represent each of those categories as a 0 or 1 and this is one way to think of that
“Although more compact coding schemes are possible, dummy variables are symmetric in the levels of the factor”
This is just them being on one and why this text can be frustrating. It’s a fancy way of saying you can use dummy variables or you can set your variables up in a different way (and assuming you do it correctly) but you’ll still get the same results
Page 10 paragraph starting with “We will typically denote…”
The next paragraphs are very dense, but it’s also the language that gets used throughout the book. The better you understand this notation, the easier of a time you’ll have reading further on. I try to provide stylized examples, but if possible, think about things in your real life you could substitute in. I’m a finance guy so I talk a lot about stocks and companies and numbers like that, but a big reason we use this book is so we can feel more comfortable thinking about numbers in our lives. This is a good opportunity to get started on that, and using it to help understand statistics better.
Scalar
A single number
10 centimeters would be an example of a scalar
Vector
A vector is a list of numbers, basically.
You can think of it as represented by:
X=[1,2,3]
Where X is the shorthand representation of a list of numbers consisting of 1, 2, and 3
If I want the first element of X, I would refer to that as
And that is equal to 1 in this case (as X=[1,2,3], so when I’m getting the first element, it is 1)
Note, this is called a subscript. 1 is the subscript to X up there
The way that the book will use these vectors, like X above, will be as columns
This is getting a little closer to a real world example
Using vectors as columns means think of X as representing the Stock Price column i.e.
Stock Price = [100, 10, 50, 50]
The same applies for all the other columns (Dividend Paid = [10,1,5,7])
A vector doesn’t have to be a column; it can be a row:
So we could look at Big Company
X = [Stock = Big Company, Stock Price = 100, Dividend Paid = 10, Debut Status = Investment Grade]
Everything in the brackets in the point above is just representing the second row where the Stock is Big Company
That is also a vector
In fact, it’s helpful to think of them like this too
That’s just four vector columns but transposed (we’ll go into that further later too)
Continuing with the above image, we can also think of them as a Matrix consisting of those 4 vectors
Matrix
A matrix is just several vectors put together like we have above
We use a bold letter to designate them as a matrix, like X
X is the four vectors (or rows) we have above consisting of Stock, Stock Price, Dividend Paid, and Debt Status
The book makes this difficult by describing it as “a set of N input p-vectors…”
Mentally substitute with the above
our four rows, each of which is a vector
The p-vector is the 4 variables or values in each of our vectors
[100,10,50,50] for the stock prices for instance
Transposing
or Transpose
The below two are each other’s Transpose:
and they represent it as:
So the top is just transposing x, whatever x is
The next x is mirroring the language that the book uses (pg. 11 “Since all vectors…).
so that’s just saying Transpose the matrix, and then get the ith vector from it
In practice using our Matrix above, that bottom transpose is grabbing the first vector, Stock = [Big Company, Small Company, Medium Company, Median Company]
ℝ is how that’s usually represented as opposed to in the book where there’s only a duplicate line on the left part of the ‘R’
It will include . It’s just kind of table stakes for the math we’re doing so it’s important to note. ℝ means 1 number - say 1, 4.5, pi, -10.599, or anything else you can easily write down. In this book you might also see R2, R3, etc - R2 means a pair of numbers like (1, 2) , R3 means a triplet like (1.5, 2.5, 3.5), and so on
Y-hat or using the circumflex (very cool name)
We can put that circumflex or hat, whichever term you prefer, to denote that we’re making a prediction so doing that for Y, X, K (or any variable)
So the above you could imagine us using when we’re predicting with an equation/model what we think Y should be with inputs X. Ditto for the others.
i.e. it might be y-hat = x1 + x2
Imagine it’s a model with two independent variables where we’re predicting a dependent variable of the change in a stock price by how much the market is up or down the current day + the stock’s sentiment (how people write about it, for instance). Then that might look like:
stock price change (y-hat) = market factor (x1) + stock news sentiment factor (x2)
Then we’ll compare how close y-hat is to actual y (aka our data on what the actual outcomes are
Using Big Company from above, we know the stock price is at 100 and we want to predict how much it will change
I will assume the market will be up 1% tomorrow
For the stock news sentiment, I have a program that looks on Twitter and sees if people are talking about Big Company in a positive or a negative manner. Then that sentiment number is converted via an algorithm* into a predicted effect on the stock.
*This is a stylized example, but it is also something that people do in real life, and understanding statistics helps you be able to assess your model better, and be able to understand results and if they fit the real world well
I used the algorithm above and it predicts based on overnight tweets, the effect on Big Company stock will be positive .5% (50 bps in finance parlance)
So our equation is y-hat = 100*.01 (or 1%) + 100*.005 (or .5%)
The Δ stock price simplifies to $1 + $.50 = 1.50 and if the y-hat equals the actual y - so in reality the stock did go up $1.50 on the day we were predicting - then that means our model was perfect in that instance
Δ is pronounced delta and although it isn’t used in this chapter, it’s a helpful math symbol to know
So the above shows the pitfalls and advantages of taking a more “practical” approach to writing about statistics. Hopefully it’s easier to read than the dense text throwing a bunch of x subscript i, N vectors, etc. but the limitation is I did do several jumps in units and assumptions
Like I knew that if you’re doing a prediction (y-hat) like this, one way to structure it is to use the coefficients as a percentage of the stock price, hence why we multiplied the 1% and .5% by 100 as that’s Big Company’s stock. If it was Medium Company, and it had the same market and sentiment assumptions it would be
Δ Medium Company Stock Price = 50*.01 + 50*.05 = .5 + .25 = .75 so it’s predicting it’ll close at 50.75 tomorrow, but the actual y could be $.50 and it closes at 50.50
I’m getting ahead, but that 25 cent difference between our y-hat and the actual y (the stock closing only up 50 cents vs predicted 75) would be called the residual
They’ll use G-hat when it’s a class label (i.e. you’re classifying a company as a Buy, Hold, or Sell - different classes)
If that was only a two-class G, then you can just use a scale of 0 to 1. Then imagine it as a y-hat problem where we know the that the output of our equation will be never be below 0 or above 1, and if the y-hat is .5 or greater then we’ll give it the 1 classification
So now we’re trying to choose if we’ll buy a stock or not; we do not own it, so there’s no hold option
That’s a binary option where the two choices are buy or hold
We now have a y-hat equation where we’re trying to determine to buy or hold, and we assume in this equation
If the y-hat value is 0.5 or greater, we will classify it as a 'buy' decision
If the y-hat value is less than 0.5, we will classify it as a 'hold' decision
Training Data is just the data we’re feeding into our equations. That matrix up above consisting of the vector columns of Stock Price, Company, etc. could be called training data
The above is really tough. But unfortunately, it’s also pretty important. The better you can understand this terminology, the easier a lot of the rest of this will be. Vectors are incredibly important as are matrices (the plural of matrix). Vectors and matrices are very important in linear algebra, which is adjacent to, and used often in statistics. We’ll try to simplify the concepts and talk through them without turning this into a linear algebra course, but just being able to think about vectors as large sets of numbers, and then matrices as large sets of vectors, then the easier this will be. With statistics and machine learning, there are so many vectors that it can become difficult to easily visualize them. Furthermore, the authors don’t take it easy on us! They give us a lot of equations, but unfortunately, they give us much fewer examples. But on the other hand, as I’m trying to put this into plainer words, I do bet they appreciate they don’t have to think of good examples that make sense.
Even though it might take a few re-reads over those pages and just trying to imagine practically what they’re saying and then looking at the examples above and even try and convert it to relevant life experience of yours that involves numbers. The good news is that if you absorb the above terminology, even when the equations start to get harder and more dense, you’ll have a fighting chance between the prose and just being able to read the equations of what they’re trying to express.
2.3 Two Simple Approaches to Predictions: Least Squares and Nearest Neighbors
2.3.1 Linear Models and Least Squares (Page 11 - 14)
We know our y-hat is our prediction.
We then have Beta (what that b is) - hat_0 (also below)
This is the intercept or known as the bias. So we’re actually seeing that this is familiar to the equation with out stock predictor above. We had:
predicted stock price Δ (y-hat) = market factor (x1) + stock news sentiment factor (x2)
But let’s change it up slightly:
predicted stock price (y-hat) = 1 * current stock price + market factor (x1) + stock news sentiment factor (x2)
1*current stock price is the intercept in this equation or the predicted beta_0
A way of thinking about it that was helpful for me was that if x1 and x2, our two independent variables equaled 0 (aka no predicted effect), then our predicted stock price would be equal to the current stock price
Next, we have:
This is just a fancy way of saying: within a bunch of columns, give us a coefficient beta-hat for each of them.
It’s easier to use an illustration (please note, this is all just made up data, but we could in fact apply these techniques on small sets like these)
Here we’re trying to predict the stock price as earlier and this is Matrix X, consisting of those vectors (columns: Stock, Stock Price T_0, etc.)
Our dependent variable or y-hat is Stock Price T_1 as that’s what we’re trying to predict
Our input or independent variables are the News Factor and Market
For market it’s the change in the overall market, so in this dataset it only covers 1 day, and the market was up 10% that day, so it’s the same for each company
The X_j is just each of those vectors (News Factor and Market), and beta-hat is going to be the coefficient (some number or scalar) that gives us the best y-hat
We’ll get into how to get the best y-hat later.
Our intercept is Stock Price T_0
Because if News Factor and Market are both 0, then (this is a large assumption) Stock Price T_1 will equal Stock Price T_0
So we have:
y-hat (our model’s predicted Stock Price T_1) = Stock Price T_0 * 1 + News Factor * beta_1 - hat + Market * beta_2 - hat
And we’ll end up trying to calculate beta_1 - hat and beta_2 - hat that ensure that the y-hat we’re predicting, comes as close as possible to the actual y, the Stock Price T_1 column
(2.2) is just saying
Stock Price T_0 in the list of beta hat coefficients (so in our case we have beta hat coefficients = [beta_1 - hat, beta_2 - hat])
X Transpose is just the list of all those variables going into our equation (Stock Price T_0, News Factor, Market)
The rest of that paragraph top of 12 is a little extra
y-hat doesn’t have to be a vector - a single number - but in fact can be a vector or a list of numbers.
The stuff with hyperplane and dimension space can be okay to think about and try to understand but it’s basically just re-elaborating that we’re including the intercept or the bias (Stock Price T_0) in our equation
(2.3) is a good equation and how we’re getting our best y-hat via the best beta hat coefficients
Calling it a quadratic just means the highest power anything is raised to is the second power aka the fact the equation is squared
This can be helpful for ensuring you have a positive number
But it also means there could potentially be more than one solution because negative numbers are included (not that important to remember)
The X transpose in the parentheses * beta is basically plugging in various numbers for the coefficients in our equation below and you can think of it as a y-hat for that equation
y-hat (our model’s predicted Stock Price T_1) = Stock Price T_0 * 1 + News Factor * beta_1 - hat + Market * beta_2 - hat
So the basic idea is to minimize the difference between the actual y and the y-hat we have (and then square it)
I have Examples Incorporated and we’re going to test the how well our equation works
I magically generated the below equation
y-hat (our model’s predicted Stock Price T_1) = Stock Price T_0 * (1 + News Factor * .05 - hat + Market * 1)
So I just replaced the beta hats with the calculated coefficients and it’s slightly different where I’ll just multiply the stock price by the sum of the News Factor and Market multiplied by their Beta-hats
I test the above with Examples Incorporated = [Stock Price T_0 = 100, News Factor = 2, Market = .10 or 10%]
y-hat = 100*(1 + 2 * .05 + .1 * 1) = 100*(1 + .1+ .1) = 100*(1.20) = 120
And then we look to see what the stock actually did on that day, our y, and it was 115
In that case, we would have a residual of (115 - 120) ^2
Which you’ll notice is applying the equation from above on RSS
What you’re doing when you run a linear regression is you’re telling the computer to do the above (the 115-120 squared) and it’s running that equation with a bunch of different beta hats until it reaches the best fit over however many X or inputs you provided
(2.4), (2.5), (2.6)
I don’t think the solution is easiest to characterize in matrix notation
Really high level, and stylized, basically it’s talking about some ways if we can know if there is a unique solution that gives us the best y-hat, or if there are multiple sets of beta hat coefficients that can minimize y - y-hat
Basically, we’re solving an optimization problem by setting the derivative equal to 0
You might recall doing this in calculus
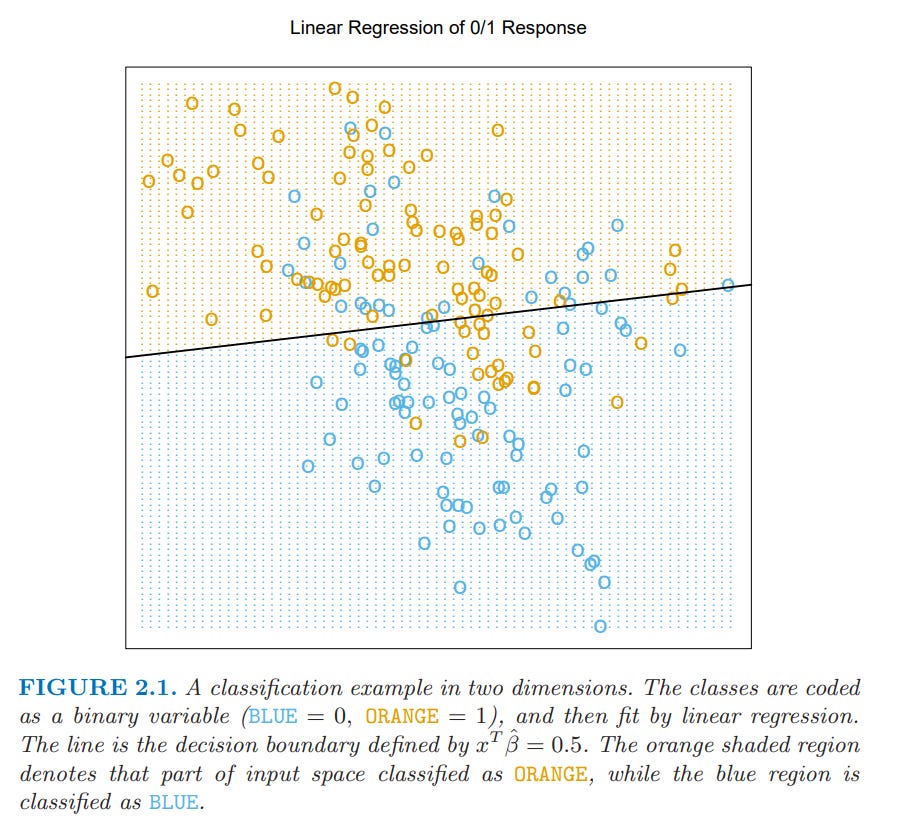
Paragraph “Let’s look at an example of the linear model…”
We are trying to predict if any given dot should be Blue or Orange; that’s the y-hat we’re trying to calculate
Plugging the numbers into our equation, whatever they are, we will get a y-hat, and if that y-hat is greater than .5 it will be orange; otherwise it’s blue
From there “Orange corresponds to {…” it’s just repeating that the y-hat for whatever the input was is greater than .5
So looking at the above figure, you can see it does pretty well in classifying the blues vs orange
But we can also see there are cases it misses too
Such is modeling
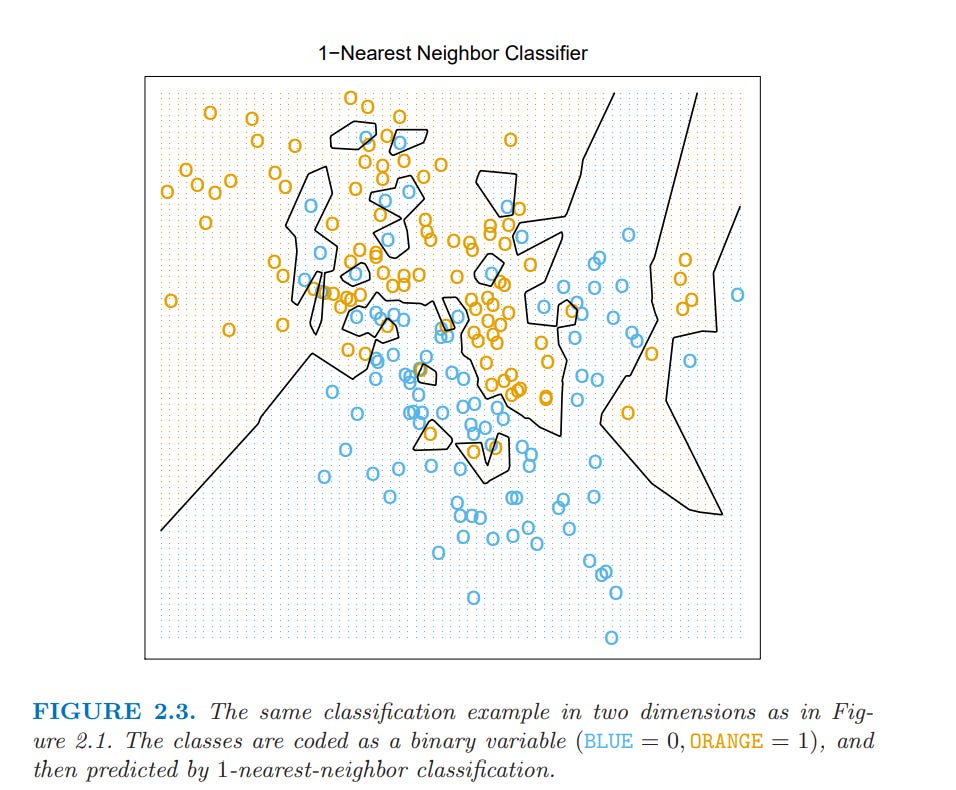
If we had an algorithm/model that captured every single dot and correctly classified them, that’s fine, but imagine trying to apply it to a different dataset. You can imagine that because it’s so fine tuned to this dataset (think of how it would have to capture the blue and orange dots NOT classified correctly above) that it would perform poorly with a different dataset. That’s what overfitting is.
In other words, do you think that the algorithm used in the below figure to correctly classify every dot would perform well on a different data set? Almost certainly not! Overfitting
From “Scenario 1:” and onwards, read it if you want. Ignore it if you please.
Getting an idea on what Gaussian distributions, and the various other jargon it throws around or permutations might be really relevant to you, but it might also not.
We did it. Part 1 done.
Hopefully now you’re feeling more comfortable with some mathematical language, and have a little bit of a better idea of what a basic Linear Model is, and how they’re calculated.
Let me know if there was anything unclear, or if there’s any ideas on how to improve the formatting. If not? Looking forwards to the next post that you can expect…eventually. Subscribe and it’ll be in your inbox!
PS
This is a really good post that someone sent me recently. I think if you start to get a good hang of this section of the book, then this is a nice companion piece in part
https://ryxcommar.com/2019/09/06/some-things-you-maybe-didnt-know-about-linear-regression/