Beyond the Joi: Quantifying Mid Maegashira and Below

Part 1

If you follow the financial news long enough, you’ll likely encounter an article about how a large move in the markets was a 5 sigma event. In this case they’re using sigma interchangeably with standard deviation - whose symbol is σ, which is pronounced sigma. They usually follow that up by saying that such an event should only occur once every million years or so. However, you see articles like these quite often. So what gives?

Well, the long and short of it is that they are using the standard deviation of a normal distribution. If you’re not familiar with a normal distribution, it’s essentially a distribution of data that occurs quite often in our world, so much so that it’s called the normal curve; it’s also known as a Gaussian Distribution or a bell curve. Check out a graph of the normal curve/distribution below courtesy of an open source stats textbook.

Part of why we use the normal distribution even though we know that it does not accurately model much financial data is because it provides a common language. In fact, the normal distribution is used often for pricing volatility, which is quite important for pricing options. Even though it isn’t accurate, it’s extremely useful. Using that assumption allows us to talk to each other in finance in a way that otherwise would be nigh impossible without the assumption.

I know I do statistics education as part of this blog, but you’re probably wondering what this has to do with Sumo. Well today I’m proud to debut a new framework that I think will be used quite a bit going forwards. Just like the normal distribution, it almost certainly isn’t perfect, but it will give us the tools to all be talking in the same language. Furthermore, now that we have the framework, we can build on top of it and do some very cool stuff as a result.

What is the Joi?

For a recent piece I was doing research on what exactly the Joi really is. We all know that it represents the top of the Banzuke, and the Japanese Kanji for it confirm as much; it’s 上位 with the first character being for “top/above” and similar connotations, and the second being position. So it’s the upper positions essentially. In fact, Wikipedia summarizes it well, based on my research: “'High rankers'. A term loosely used to describe wrestlers who would expect to face a yokozuna during a tournament.”

So our goal here today is to try and use numbers in order to pin down what the Joi is, or at least provide one possible definition of the Joi. Before we do that though, let’s talk about why we would want to do that.

Why Is Knowing the Joi Important?

There’s more work to be done on using algorithmic prediction of daily matches, but generally speaking we know that where you are ranked within the Banzuke will affect who you are matched up against. For the top two divisions, guys near you will be who you fight the first week or so. For the lower four divisions, the first two matches you fight will be guys right next to you on the Banzuke (and then it’s based on record, as is the second week or so for Makuuchi and Juryo - the top two divisions).

So during my Ozeki and Yokozuna previews the past couple tournaments, I’ve consistently referred to how we’re looking at a much more talented Joi. We have more Ozeki and former Ozeki alongside up and comers like Onosato and now Hiradoumi who have shown they can stick around at the top. That’s very important, because when you’re consistently facing more talented guys, wins are much harder to come by.

But What About Beyond the Joi?

Just as the Joi is rather loosely defined, once you get beyond the Joi, defining similar ranges like mid-Maegashira, lower Maegashira, Upper Juryo, and so on gets even harder. In fact, does it make sense to have an Upper Juryo, Middle Juryo, and Lower Juryo? Should there be more ranges in the Juryo, or fewer? What about the lower divisions?

Today I will seek to answer exactly these kinds of questions. This is quite relevant as you’ll often see hot prospects hit a wall and their previous 6-1’s or 7-0’s in the bottom divisions of Jonokuchi, Jonidan, and Sandanme¹ become 3-4’s or worse when hitting the mid-Makushita. This is something I have noticed previously, but now today I seek to provide the framework to actually define what “mid-Makushita” might be.

How Does This Work?

As usual, I am using data from 1988-2023. As a refresher, that was right after Futahaguro was forcibly retired from Sumo. It’s a story worth checking out on his Wikipedia as he’s infamous for not only that forcible retirement, but also being the only Yokozuna to never win a Yusho. It serves as a neat cut-off point for what I classify as “modern Sumo.”

That data from 1988 onwards is every single individual match including an identifier for the Basho and which day of the Basho it was on. So the Hatsu Basho in 1988 on the first day would have a key something like 19880101 (1988 - January - Day 1). Once I gathered all those matches, I then also assigned the Absolute Rank based on individual wrestler’s rank in the Banzuke agnostic to division. So the Yokozuna 1 East at the top of the Banzuke has a rank of 1. A guy that’s in Makushita will have a rank that’s something like 100 or so.

To begin with, I started by trying to define the Joi. I began with the top ranked wrestler in each tournament and looked at all their matches. I then made a set of all the opponents they faced by rank. So that looks like this for the top ranked wrestler in my data.

Then I filter through that list, going rank by rank and checking how many times they faced off against wrestlers with Absolute Rank 2, then 3, and so on. I do this day by day, and divide by how many total matches they have on any given day. That is the likelihood they’ll face a wrestler with that rank on that day. Add those up over those 15 days and you have the likelihood a wrestler at a given rank will face a wrestler of another given rank in any tournament. It might make more sense with an image showing the calculations for wrestlers with Absolute Rank 1.

As you can see the top wrestler only faces the second ranked wrestler on the last two days, and really, just the final day.

Next I do this for each rank of opponent that the top wrestler has faced which gives me output that looks like the below. I truncated the output to make it easier to read, but it covers more than just ranks 2, 3, and 4. The number that follows after is the cumulative likelihood so 2 is faced 72.75% of the time and so on.

So now we have some solid data to work with and here comes the hard part. How do we interpret it?

I began this piece with some stats education and I would like to carry that over to here. In fact, it is directly relevant to a recent debate I have seen regarding statistics: how do we interpret them? In the sciences, people often use a P value of .05 as the threshold for significance. We need not go into P values today, but the point is that some are questioning if using .05 as the cut-off for a study being significant or not is proper. The detractors have a solid point: .05 as a P value doesn’t guarantee that results are significant. It certainly makes it more likely that results are significant, but nothing in life is guaranteed. Not just with P values, but in life in general we are often faced with having to set relatively arbitrary boundaries and definitions. .05 is a nice round number in our eyes, and serves are purposes generally well, but if we used .04 we might have some additional benefits (and consequences) just the same as if we used .06.

Essentially, my point is that I used some decently arbitrary thresholds to define these ranges. In fact, it goes back further than here; the choice of using 1988 post Futahaguro retirement for my data set is also arbitrary. In fact, for more stats education: generally speaking in statistics, arbitrary isn’t a bad word. We’re used to hearing something described as arbitrary and it means that was bad. In this case, when we call it arbitrary it means “we could have used some other dataset, or some other threshold, but we ultimately decided to go with the ones we went with.” I just wanted to point this out for this exercise, and in case someone wanted to do some similar kind of analysis like this - by no means do you have to use these exact same numbers, and perhaps using different ones would be better. Sometimes in statistics we have to use arbitrary thresholds just like the .05 for P values above. With that out of the way, continuing on.

For the Joi and Makuuchi in general, I organized each band by looking for ranges where 50%+ of the time in each tournament a wrestler would have an opponent. In other words, my first range, the Joi is defined by wrestlers that would have a 50% or higher likelihood to face the wrestler with an Absolute Rank of 1 in a tournament. It looks like this with 17 being the final rank included in this Joi I calculated.

Using this framework - I went through the entire Banzuke to Makushita for Part 1 today. Part 2 will cover Sandanme and Jonidan, but likely not Jonokuchi as it essentially consists of guys who have just debuted or who have been missing lots of matches due to injury. So I’ll just have Jonokuchi as it’s own range unless I come up with a better methodology.

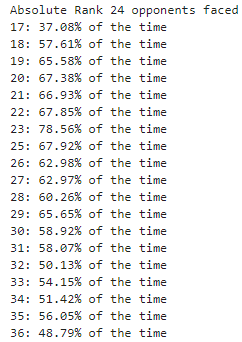
However, once we go beyond the first range of the Joi, the methodology changes slightly. With the Joi, what we care about is the top ranked wrestler and who is facing them, but if I started with the 18th ranked wrestler (the first one not included in this Joi) then it would end up overlapping significantly. So instead what I did was run the numbers until I found the next exclusive range. Again, I think seeing helps, so for finding the Mid Maegashira/2nd range I ended up with the 24th ranked Rikishi (wrestler) which does not include the 17th ranked wrestler but does include the 18th. This gives a Mid-Maegashira range from 18-35.

Hopefully by now this makes sense. For the rest of the ranges, I’ll include the ranks, and also who would book end them to make it easier in practice. As a final note, I did play with the percentages beyond the Makuuchi a bit. For instance, I use a higher threshold for Juryo to split it up better. Conversely, with the lower divisions I actually had to lower the threshold to have it work. Everything will be spelled out, but as I said at the start: the goal here is to have a coherent framework that we can then use further.

Makuuchi - 50% Threshold

Joi - Range 1: 1-17, Y1E Terunofuji - M4W Kotoshoho

Mid Maegashira - Range 2: 18-35, M5E Ura - M13W Nishikigi

Lower Maegashira - Range 3: 36-42, M14E Ryuden - M17E Nishikifuji

Juryo - 60% Threshold

Upper Juryo - Range 4 = 43-58, J1E Chiyoshoma - J8W Hakuyozan

Lower Juryo - Range 5 = 59-70, J9E Daishoho - J14W Oshoumi

Makushita - 30% Threshold

Elite Makushita - Range 6 = 71-87 Ms1E Tsukahara - Ms9E Kotokenryu

Near Elite Makushita - Range 7 = 88-105 Ms9W Kamito - Ms18E Tanji

Upper Intermediate Makushita - Range 8 = 106-122 Ms18W Tokunomusashi - Ms26W Kanzaki

Intermediate Makushita - Range 9 = 123-140 Ms27E Fujinoyama - Ms35W Wakatakamoto

Lower Intermediate Makushita - Range 10 = 141-157 Ms36E Narutaki - Ms44E Kaigo

Lower Makushita - Range 11 = 158-176 Ms44W Kazenoumi - Ms53W Hoshuzan

Bottom Makushita + Top Sandanme - Range 12 = 177-195 Ms54E Marusho - Sd2W Hatooka

Thanks for reading and I hope to have Part Two next week or if not the next couple weeks.

1. The three lowest divisions going from lowest in the Jonokuchi to highest in Sandanme