Predicting Sumo Retirement - Using Statistics

With some basic numbers, can we predict when wrestlers will retire?

One big question for now now is: when will Terunofuji retire? In fact, when will any wrestler retire? Well this is a question we have data on, and I had some ideas on how to model. So sit back and I’ll go over the basics at the top and then present the numbers, and then if you want some more Model Talk, then just keep reading on to the Model Talk section and we’ll talk about why I didn’t use a linear regression and other stats stuff.

So our dataset covers from 1988-2023 and consists of every wrestler’s records from Makuuchi to the bottom division Jonokuchi. If someone retired, then they have a 1 to represent they retired. If they didn’t retire in that tournament, then that will be represented with a 0. What we’ll be doing today is putting a percent chance that a wrestler will retire (or be coded a 1, using the language of our model).

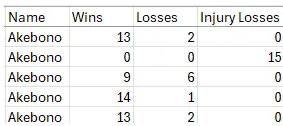
I used 3 different features or input variables to help determine if a wrestler will retire or not. First we have age. Hopefully that’s self explanatory, but I took each wrestler’s birthday and then calculated their age as of the tournament. Second we have Cumulative Injury Loss %. If you’re in the top 2 divisions, you fight 15 times; the bottom 4, you fight 7 times. So I just took what percentage of those losses were due to injuries; which in this case is whether they participated in a match or not as expected.¹ The final feature is Demoted. I looked if a wrestler had been demoted or not in the past tournament. This is what a subset of Akebono’s career looks like to give a good idea.

I initially modeled it with 3 tournaments worth of Cumulative Injury Losses and whether you were demoted or not (were you demoted past 3 tournaments), but it turns out that just using 1 tournament is actually better for prediction. Just wanted to clarify that and why it’s called Cumulative Injury Losses. Really it’s just one tournament.

So now that we have a good idea what goes into the model, let’s take a look at the results themselves:

What does this mean? Well, when you’re using this with your inputs, it’s actually slightly different from our linear regression so let’s say we have a 40 year old wrestler Exampleyama, who missed 80% of the recent matches but has not been demoted. Then we’d calculate it as follows

step 1: -12.4543 (constant) + .2412 * 40 + .8 * 3.8403 + 0 * .4689 = 1.034

step 2: y-hat (percent chance predicted he’ll retire) = 1 - 1/(1+e^(1.034))

y-hat = 0.737691 or ~74%

I think that seems about right and if you assume Exampleyama did get demoted then it goes to 82%. Seems like what we’d expect.

So we know how to use these results, but how good are they? Well, looking at our Pseudo R-squared, our model can explain ~35% of the sample. That’s not quite like when we did Banzuke prediction and were able to get an R-squared more like 75%.

I excluded the Yokozuna because they’re subject to different constraints (like do we think Terunofuji retires until there’s a new Yokozuna? I don’t. They can’t get demoted either). I actually ran the numbers with and without them and it made essentially no difference but R-squared down slightly.

I have been thinking of different features (input variables) I could test and nothing is sticking out to me. I might try looking at losses, but in theory, Demoted should capture that. If you’re losing a lot, you’ll be demoted, and we also have Injury Losses included. I think what recommends using demoted instead of (regular) Losses, is that unless you’re too banged up to wrestle (captured via Cumulative Injury Losses), you’ll be tempted to try and go one more tournament in the paid ranks. I also have a trump card that I ran it with losses included and it didn’t seemingly improve the model very much.

I also limited the dataset to wrestlers who reached Juryo or Makuuchi. I think someone who reached the paid ranks is different to someone who is more a lower ranks lifer. In fact, when I was using 3 tournaments worth of data for Injury Losses and Demotion, prior to excluding the lower divisions, the formula had it making you less likely to retire if you got demoted.

The data backs me up on those two as those exclusions got me from a Pseudo R-squared of ~32.5% up to our 35.5%. That’s not nothing! Check out some data covering the dataset I ended up using.

In a perfect world, I would have crowdsourced predictions of who will retire each tournament, a-la Guess the Banzuke. As of now, there just isn’t a metric to compare our R-squared to. However, I think it’s a good start. I think it’ll be interesting to see how else this can be improved. If I have any updates I’ll be sure to follow up.

I will provide the calculations for everyone in the top 10 most likely to retire after the last tournament below. Technically, they should all be 0 other than Hokuseiho as nobody else in the top two divisions retired, but it’ll give us a nice preview of who we might expect to retire in the future. Check it out, it actually had Hokuseiho as likely to retire despite his young age. His losses because he’s retiring in the code logic got interpreted as injury losses, so if anything, kinda neat it in a certain way captured his demise. Since I’m writing this in May, as soon as the tournament is over I’ll immediately update and publish the rankings, although I suppose I gave up the formula so feel free to run it for whomever individually you want if you think it’s worthwhile.

Model Talk

So I like to try and do some statistics and “under the hood discussion” too. The Banzuke rankings are linear because it’s giving each wrestler a score on how well they did in the tournament. Then they’re ordered by score, and that gives us the Banzuke. We use a function that is a line you can extend infinitely, in theory, if you wanted to. We don’t care in this case, but it can be helpful in other situations which is good to know.

However, retirement is a binary thing: you either retire or you don’t. So we’re using a logistic regression, because it then bounds us between the 0 of not retiring, and the 1 of retiring. And doing that is helpful because we can then calculate a function that explains retirements with a percentage. Check out the Wikipedia image for a logistic regression.

²

I initially used a 3 tournament period for the cumulative injury loss totals and the binary variable on if you were demoted. I thought 1 was probably a little too inflexible and 4 felt like too long. However, I was wrong. I turns out, really what matters the most is tournament to tournament.

I was initially at ~18-19% R-squared, and moving to just the most recent tournament, limiting to Juryo + Makuuchi, and no Yokozuna got us to 35.5%. Almost double; very neat! That said, I do think I’ve gotten the low hanging fruit. I ran it with Losses as a feature, and that only bumped up the R-squared to 36% - given I do think it’s collinear with Demoted, I opted to keep that out for the version I ran. I think that tradeoff from potential overfitting vs. a half percent of R squared just isn’t worth it.

Another feature I ran the model with was a reader’s suggestion of their rank. So basically, the lower down the Banzuke you are, will that make you more likely to retire (again, for sekitori)? I think it has a very sound foundation to influence a wrestler: if you’re lower down the Banzuke that’s just inherently demoralizing. So I did run it with that as an additional feature and it moved the R-squared up about .1% so unfortunately like Losses, it seems with our current features we’ve probably captured any explanatory power of that additional variable.

One idea I do have is potentially fitting the three tournament window but as an exponential moving average; so we would get some data from prior tournaments, and in theory it ought to give us a more accurate picture of what goes into a retirement decision but we would also be weighing the most recent tournament most heavily. That could be the best of both worlds. Other than that, I can’t think of any particularly good techniques or features off the top of my head that would move the needle. As always, if you do, feel free to reach out and thanks for reading.

1. This means that Fusen losses aren’t included as injury losses, but they constitute a really small percentage of matches I know from my dataset. I think it was less than half a percent; it shouldn’t move the needle too much, and it’s also one of 3 features. Just wanted to note this because it is a limitation for this exercise

2. https://en.wikipedia.org/wiki/File:Exam_pass_logistic_curve.svg